What’s a Tangram?
A tangram is an ancient Chinese puzzle made of seven flat geometric shapes, called “tans”: five triangles of different sizes, one square, and one parallelogram. Together, these pieces form a perfect square. Rearrange them, and you can create thousands of shapes that look like people, animals, or objects. Some tangram sets, like those forming an egg shape, use different pieces, but Tangram Fury sticks to the traditional seven-piece design.

What’s a Polygon?
A polygon is a flat, closed shape with three or more straight sides—no curves allowed! Think triangles, squares, or even an octagon like a stop sign. Circles and ovals don’t count because of their rounded edges. Polygons are classified as “simple” if their sides don’t cross (like a square) or “complex” if they do (like a star).

Are All Tangrams Polygons?
Yep, pretty much! Since tangram puzzles use seven flat-sided pieces (tans) that touch without overlapping, the shapes they form are polygons. Some are simple (like a basic house shape), while others are complex (like a person running). They might look like bunnies or boats, but they’re just polygon shapes suggesting those things.

What is a Convex Polygon?
Alright, let’s keep this fun and simple. A convex polygon is a rare type of shape where every side bulges outward, like a puffed-up beach ball (but with flat sides, since it’s a polygon). Imagine rowing across a lake: if you can paddle straight from any point on the shore to any other without hitting having to turn the canoe, then that lake is convex. If the shore caves in, it’s concave.

What’s a Concave Polygon?
Think of a concave polygon as a shape with a “dent” in it, like a caved-in wall. Unlike a convex polygon, which bulges out (imagine the puffed-up beach ball), a concave polygon has at least one angle that dips inward, making it look like it’s got a bite taken out of it. For example, picture the outline of a star or a crescent moon shape—those are concave because their edges cave in. Technically, one of its angles is over 180 degrees, but just think “dented shape” and you’re good!

OK, let’s try one last example to make sure this is clear. Picture a deflated beach ball. When it’s deflated, you can grab it because parts of it are tucked into itself, or there are dents in its surface, or however you want to describe that. Now, just picture the deflated beach ball’s shadow (because polygons aren’t 3-dimensional). Because of the dents in the edges of the shadow, the deflated beach ball’s shadow is concave. Fill that ball with air, and the shadow will be convex. (But, it won’t be a polygon, because it’s round….) Using this analogy, one could say that a convex polygon is a flat-sided shape that is essentially bursting at its seams.

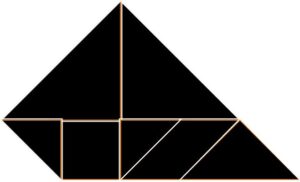
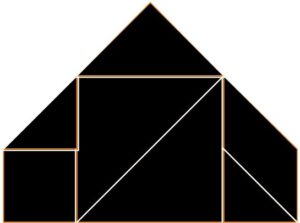
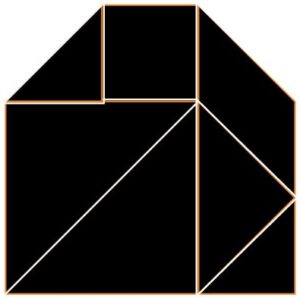
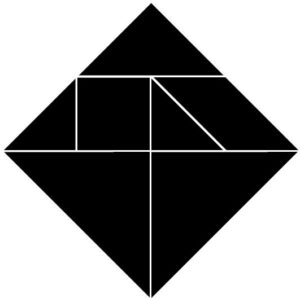
What’s a Convex Tangram?
A convex tangram is an extremely-rare tangram shape that’s also a convex polygon—meaning it’s all puffed out with no dents. In 1942, mathematicians Fu Traing Wang and Chuan-Chin Hsiung proved mathematically that out of thousands of possible tangram shapes made with the seven tans, only 13 are convex polygons. That’s a tiny fraction! Tangram Fury includes all 13, some named “pyramid” or “tent,” but most labeled as “Convex Tangram.” Spotting these in the game is like finding a rare treasure while you race to win!